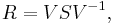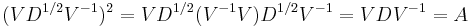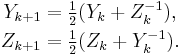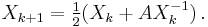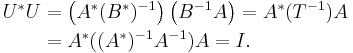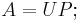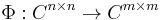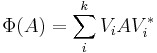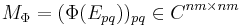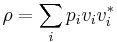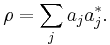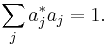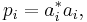Square root of a matrix

In mathematics, the square root of a matrix extends the notion of square root from numbers to matrices. A matrix B is said to be a square root of A if the matrix product B · B is equal to A.^[1]

1 Properties
2 Computation methods
3 Square roots of positive operators
- 3.1 Unitary freedom of square roots
- 3.2 Some applications
4 See also
5 Notes
6 Bibliography

Properties

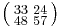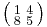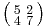In general, a matrix can have many square roots. For example, the matrix $\bigl( \begin{smallmatrix}\\ 33&24\\ 48&57\end{smallmatrix} \bigr)$ has square roots $\bigl( \begin{smallmatrix}\\ 1&4\\ 8&5\end{smallmatrix} \bigr)$ and $\bigl( \begin{smallmatrix}\\ 5&2\\ 4&7\end{smallmatrix} \bigr)$ , as well as their additive inverses. 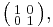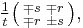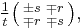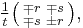Another example is the 2×2 identity matrix $\bigl( \begin{smallmatrix}\\ 1&0\\ 0&1\end{smallmatrix} \bigr),$ which has an infinitude of symmetric rational square roots given by $\tfrac{1}{t}\bigl( \begin{smallmatrix}\\ \mp s&\mp r\\ \mp r&\pm s\end{smallmatrix} \bigr),$ $\tfrac{1}{t}\bigl( \begin{smallmatrix}\\ \pm s&\mp r\\ \mp r&\mp s\end{smallmatrix} \bigr),$ $\tfrac{1}{t}\bigl( \begin{smallmatrix}\\ \mp r&\mp s\\ \mp s&\pm r\end{smallmatrix} \bigr),$ $\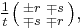tfrac{1}{t}\bigl( \begin{smallmatrix}\\ \pm r&\mp s\\ \mp s&\mp r\end{smallmatrix} \bigr),$ $\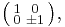bigl( \begin{smallmatrix}\\ 1&0\\ 0&\pm 1\end{smallmatrix} \bigr),$ and $\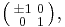bigl( \begin{smallmatrix}\\ \pm 1&0\\ 0& 1\end{smallmatrix} \bigr),$ where (r, s, t) is any Pythagorean triple — that is, any set of positive integers such that 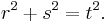$r^2 %2B s^2 = t^2.$ ^[2]

However, a positive-definite matrix has precisely one positive-definite square root, which can be called its principal square root.

While the square root of an integer is either again an integer or an irrational number, in contrast an integer matrix can have a square root whose entries are rational, yet not integral. For example, the matrix 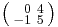$\bigl( \begin{smallmatrix}\\ ~\;0&4\\ -1&5\end{smallmatrix} \bigr)$ has a square root 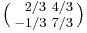$\bigl( \begin{smallmatrix}\\ ~\;2/3&4/3\\ -1/3&7/3\end{smallmatrix} \bigr)$ , as well as a square root that is an integer matrix: 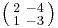$\bigl( \begin{smallmatrix}\\ 2&-4\\ 1&-3\end{smallmatrix} \bigr)$ . The other two square roots are the additive inverses of these (In general, a 2×2 matrix with two distinct eigenvalues has four square roots). The 2×2 identity matrix discussed above provides another example.

Just as with the real numbers, a real matrix may fail to have a real square root, but have a square root with complex-valued entries.

Computation methods

Explicit formulas

For a 2 × 2 matrix, there are explicit formulas that give up to four square roots, if the matrix has any roots.

If D is a diagonal n × n matrix, one can obtain a square root by taking a diagonal matrix R, where each element along the diagonal is a square root of the corresponding element of D. If the diagonal elements of D are real and non-negative, and the square roots are taken with non-negative sign, the matrix R will be the principal root of D.

By diagonalization

An n × n matrix A is diagonalizable if there is a matrix V and a diagonal matrix D such that 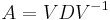$A = V D V^{-1}$ . This happens if and only if A has n eigenvectors which constitute a basis for Cⁿ. In this case, V can be chosen to be the matrix with the n eigenvectors as columns, and a square root of $A$ is

$R = V S V^{-1}, \,$

where S is any square root of D. Indeed,

$(V D^{1/2} V^{-1})^2 = V D^{1/2} (V^{-1} V) D^{1/2} V^{-1} = V D V^{-1} = A\,$

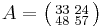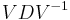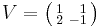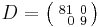For example, the matrix $A = \bigl(\begin{smallmatrix}\\ 33&24\\ 48&57\end{smallmatrix} \bigr)$ can be diagonalized as $V D V^{-1}$ , where $V = \bigl( \begin{smallmatrix}\\ 1&~\;1\\ 2&-1\end{smallmatrix} \bigr)$ and $D = \bigl( \begin{smallmatrix}\\ 81&0\\ ~\;0&9\end{smallmatrix} \bigr)$ .

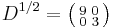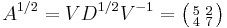$D$ has principal square root $D^{1/2} = \bigl( \begin{smallmatrix}\\ 9&0\\ 0&3\end{smallmatrix} \bigr)$ , giving the square root $A^{1/2} = V D^{1/2} V^{-1} = \bigl( \begin{smallmatrix}\\ 5&2\\ 4&7\end{smallmatrix} \bigr)$ .

By Jordan decomposition

For non-diagonalizable matrices one can calculate the Jordan normal form followed by a series expansion, similar to the approach described in logarithm of a matrix.

By Denman–Beavers iteration

Another way to find the square root of an n × n matrix A is the Denman–Beavers square root iteration. Let Y₀ = A and Z₀ = I, where I is the n × n identity matrix. The iteration is defined by

$\begin{align} Y_{k%2B1} &= \tfrac12 (Y_k %2B Z_k^{-1}), \\ Z_{k%2B1} &= \tfrac12 (Z_k %2B Y_k^{-1}). \end{align}$

Convergence is not guaranteed, even for matrices that do have square roots, but if the process converges, the matrix 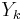$Y_k$ converges quadratically to a square root A^1/2, while 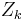$Z_k$ converges to its inverse, A^−1/2. (Denman & Beavers 1976; Cheng et al. 2001).

By the Babylonian method

Yet another iterative method is obtained by taking the well-known formula of the Babylonian method for computing the square root of a real number, and applying it to matrices. Let X₀ = I, where I is the identity matrix. The iteration is defined by

$X_{k%2B1} = \tfrac12 (X_k %2B A X_k^{-1})\,.$

Again, convergence is not guaranteed, but if the process converges, the matrix 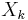$X_k$ converges quadratically to a square root A^1/2. Compared to Denman–Beavers iteration, an advantage of the Babylonian method is that only one matrix inverse need be computed per iteration step. However, unlike Denman–Beavers iteration, this method is numerically unstable and more likely to fail to converge.^[1]

Square roots of positive operators

In linear algebra and operator theory, given a bounded positive semidefinite operator (a non-negative operator) T on a complex Hilbert space, B is a square root of T if T = B* B, where B* denotes the Hermitian adjoint of B. According to the spectral theorem, the continuous functional calculus can be applied to obtain an operator T^½ such that T^½ is itself positive and (T^½)² = T. The operator T^½ is the unique non-negative square root of T.

A bounded non-negative operator on a complex Hilbert space is self adjoint by definition. So T = (T^½)* T^½. Conversely, it is trivially true that every operator of the form B* B is non-negative. Therefore, an operator T is non-negative if and only if T = B* B for some B (equivalently, T = CC* for some C).

The Cholesky factorization provides another particular example of square root, which should not be confused with the unique non-negative square root.

Unitary freedom of square roots

If T is a non-negative operator on a finite dimensional Hilbert space, then all square roots of T are related by unitary transformations. More precisely, if T = AA* = BB*, then there exists a unitary U s.t. A = BU.

Indeed, take B = T^½ to be the unique non-negative square root of T. If T is strictly positive, then B is invertible, and so U = B⁻¹A is unitary:

$\begin{align} U^*U &= \left(A^*(B^*)^{-1}\right)\left(B^{-1}A\right) = A^*(T^{-1})A \\ &=A^*((A^*)^{-1}A^{-1})A = I. \end{align}$

If T is non-negative without being strictly positive, then the inverse of B cannot be defined, but the Moore–Penrose pseudoinverse B⁺ can be. In that case, the operator B⁺A is a partial isometry, that is, a unitary operator from the range of T to itself. This can then be extended to a unitary operator U on the whole space by setting it equal to the identity on the kernel of T. More generally, this is true on an infinite-dimensional Hilbert space if, in addition, T has closed range. In general, if A, B are closed and densely defined operators on a Hilbert space H, and A* A = B* B, then A = UB where U is a partial isometry.

Some applications

Square roots, and the unitary freedom of square roots have applications throughout functional analysis and linear algebra.

Polar decomposition

Main article: Polar decomposition

If A is an invertible operator on a finite-dimensional Hilbert space, then there is a unique unitary operator U and positive operator P such that

$A = UP;\,$

this is the polar decomposition of A. The positive operator P is the unique positive square root of the positive operator A^∗A, and U is defined by U = AP⁻¹.

If A is not invertible, then it still has a polar composition in which P is defined in the same way (and is unique). The unitary operator U is not unique. Rather it is possible to determine a "natural" unitary operator as follows: AP⁺ is a unitary operator from the range of A to itself, which can be extended by the identity on the kernel of A^∗. The resulting unitary operator U then yields the polar decomposition of A.

Kraus operators

Main article: Choi's theorem on completely positive maps

By Choi's result, a linear map

$\Phi�: C^{n \times n} \rightarrow C^{m \times m}$

is completely positive if and only if it is of the form

$\Phi(A) = \sum_i ^k V_i A V_i^*$

where k ≤ nm. Let {E_{p q}} ⊂ C^{n × n} be the n² elementary matrix units. The positive matrix

$M_{\Phi} = ( \Phi (E_{pq}) )_{pq} \in C^{nm \times nm}$

is called the Choi matrix of Φ. The Kraus operators correspond to the, not necessarily square, square roots of M_Φ: For any square root B of M_Φ, one can obtain a family of Kraus operators V_i by undoing the Vec operation to each column b_i of B. Thus all sets of Kraus operators are related by partial isometries.

Mixed ensembles

Main article: Density matrix

In quantum physics, a density matrix for an n-level quantum system is an n × n complex matrix ρ that is positive semidefinite with trace 1. If ρ can be expressed as

$\rho = \sum_i p_i v_i v_i^*$

where ∑ p_i = 1, the set

$\{p_i, v_i \} \,$

is said to be an ensemble that describes the mixed state ρ. Notice {v_i} is not required to be orthogonal. Different ensembles describing the state ρ are related by unitary operators, via the square roots of ρ. For instance, suppose

$\rho = \sum_j a_j a_j^*.$

The trace 1 condition means

$\sum_j a_j ^* a_j = 1.$

Let

$p_i = a_i ^* a_i,$

and v_i be the normalized a_i. We see that